Pohybová energie

Pohybová energie
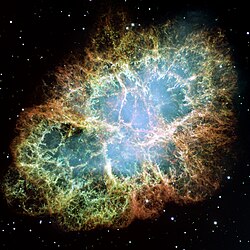	Pohybová energie plynu expandujícího rychlostí přes 1500 km/s je zdrojem záření Krabí mlhoviny.
Definice	Energie, kterou má těleso díky svému pohybu
Typ	Fyzikální veličina

Rozbalit box

Obsah boxu

Pohybová energie, odborně kinetická energie (z řeckého slova kinesis, pohyb), je forma energie, kterou má hmotný objekt nebo částice díky svému pohybu. [1] Jedná se o jednu ze dvou hlavních složek mechanické energie; tou druhou je polohová (potenciální) energie. [2] Velikost pohybové energie závisí na dvou klíčových vlastnostech tělesa: jeho hmotnosti a rychlosti. Čím je těleso těžší a čím rychleji se pohybuje, tím větší je jeho pohybová energie. [3]

📜 Historie konceptu

Pojem energie a její souvislost s pohybem se vyvíjely po několik staletí. Koncept, který dnes nazýváme pohybovou energií, má kořeny v 17. a 18. století ve vědeckých debatách o "síle pohybu".

Německý učenec Gottfried Wilhelm Leibniz v letech 1676–1689 navrhl koncept nazývaný vis viva (živá síla), který definoval jako součin hmotnosti tělesa a druhé mocniny jeho rychlosti (mv²). [4] Leibniz tvrdil, že tato "živá síla" se v mnoha mechanických systémech zachovává. Jeho myšlenka stála v protikladu k teorii Isaaca Newtona, který definoval hybnost (mv) jako hlavní míru pohybu. [5]

Debatu zásadně posunula vpřed francouzská fyzička a matematička Émilie du Châtelet. Ve své knize Institutions de Physique (Základy fyziky) z roku 1740 na základě experimentů nizozemského fyzika Willema 's Gravesanda prokázala, že energie dopadajícího tělesa je skutečně úměrná druhé mocnině rychlosti, nikoli rychlosti samotné, čímž potvrdila Leibnizovu myšlenku. [6, 7] Byla to právě ona, kdo navrhl, že kinetická energie by měla být definována s faktorem ½ (tedy ½mv²), aby byla v souladu s konceptem práce. [6] Tento moderní tvar a termín "kinetická energie" se však plně vžily až v polovině 19. století díky práci Gasparda-Gustava de Coriolise a Williama Thomsona (lorda Kelvina). [8]

⚙️ Klasická mechanika

V rámci klasické (newtonovské) mechaniky, která popisuje pohyb objektů při rychlostech mnohem menších, než je rychlost světla, se pohybová energie (E_k) vypočítá podle základního vzorce: [9]

$E_{k} = \frac{1}{2} m v^{2}$

Kde:

$E_{k}$ je pohybová (kinetická) energie,
$m$ je hmotnost tělesa,
$v$ je rychlost tělesa.

Z tohoto vzorce vyplývá klíčový poznatek: zatímco hmotnost ovlivňuje energii lineárně, rychlost ji ovlivňuje kvadraticky. To znamená, že zdvojnásobení rychlosti tělesa zvýší jeho pohybovou energii čtyřikrát, a ztrojnásobení rychlosti ji zvýší devětkrát. [10] To je důvod, proč mají vysoké rychlosti tak devastující následky například při automobilových nehodách.

Vztah k práci

Pohybová energie je úzce spjata s konceptem mechanické práce. Princip práce a energie říká, že celková práce (W) vykonaná na těleso vnějšími silami se rovná změně jeho pohybové energie (ΔE_k). [11]

$W = Δ E_{k} = E_{k 2} - E_{k 1}$

Pokud na těleso působíme silou ve směru jeho pohybu (např. tlačíme auto), konáme kladnou práci a jeho pohybová energie roste. Pokud působíme silou proti směru pohybu (např. brzdíme), konáme zápornou práci a pohybová energie klesá. [12]

Jednotky

Základní jednotkou energie je Joule (značka J). Jeden joule je definován jako práce, kterou vykoná síla jednoho newtonu působící na dráze jednoho metru. [13] V základních jednotkách SI lze joule vyjádřit jako:

$1 J = 1 N \cdot m = 1 k g \cdot \frac{m^{2}}{s^{2}}$

Tento rozměr přesně odpovídá jednotkám ve vzorci pro pohybovou energii (hmotnost × rychlost²). V částicové fyzice se často používá menší jednotka elektronvolt (eV).

🚀 Relativistická mechanika

Vzorec $E_{k} = \frac{1}{2} m v^{2}$ dokonale popisuje náš každodenní svět. Když se však rychlost objektu začne přibližovat rychlosti světla (značka c), klasická mechanika přestává platit a je nutné použít principy speciální teorie relativity Alberta Einsteina. [14]

Podle relativity se hmotnost objektu s rostoucí rychlostí efektivně zvyšuje. K jeho dalšímu urychlení je proto potřeba exponenciálně více energie. Pohybová energie v relativistické mechanice se proto počítá podle odlišného vzorce: [15]

$E_{k} = (γ - 1) m c^{2}$

Kde:

$m$ je klidová hmotnost tělesa,
$c$ je rychlost světla ve vakuu,
$γ$ (gamma) je Lorentzův faktor, který závisí na rychlosti v a je definován jako $γ = \frac{1}{\sqrt{1 - v^{2} / c^{2}}}$ .

Pro nízké rychlosti se hodnota Lorentzova faktoru blíží 1 a tento složitý vzorec se zjednoduší na dobře známý tvar $\frac{1}{2} m v^{2}$ . [16] Jak se však rychlost blíží c, Lorentzův faktor a tedy i pohybová energie rostou nade všechny meze. To znamená, že žádný hmotný objekt nemůže nikdy dosáhnout rychlosti světla, protože by to vyžadovalo nekonečné množství energie. [15]

🔄 Rotační pohybová energie

Kromě posuvného (translačního) pohybu z jednoho místa na druhé se mohou tělesa také otáčet kolem své osy. Tento rotační pohyb je rovněž spojen s pohybovou energií, kterou nazýváme rotační (či rotační kinetická) energie. [17]

Její velikost nezávisí na rychlosti těžiště, ale na tom, jak rychle se těleso otáčí a jak je hmota v tělese rozložena vzhledem k ose otáčení. Vzorec pro rotační energii je analogický k tomu pro posuvný pohyb: [18]

$E_{k}_{r} = \frac{1}{2} I ω^{2}$

Kde:

$I$ je moment setrvačnosti tělesa, který vyjadřuje odolnost tělesa vůči změně rotačního pohybu (analogie hmotnosti),
$ω$ (omega) je úhlová rychlost tělesa (analogie rychlosti).

Celková pohybová energie tělesa, které se zároveň posouvá a otáčí (např. kutálející se koule), je součtem jeho posuvné a rotační pohybové energie. [19] Rotační energii mají planety, roztočené setrvačníky, kola automobilů nebo vrtule.

⚛️ Formy a projevy pohybové energie

Pohybová energie se v přírodě projevuje v mnoha různých formách a měřítkách.

Tepelná energie

Tepelná energie látky je ve skutečnosti součtem mikroskopických pohybových energií všech jejích neustále a neuspořádaně se pohybujících atomů a molekul. [20] Teplota je pak fyzikální veličina, která je přímo úměrná průměrné pohybové energii těchto částic. [21] Čím rychleji se částice pohybují (vibrují, rotují, posouvají se), tím vyšší teplotu látka má. Tento princip popisuje kinetická teorie látek.

Energie proudění a zvuku

Makroskopické projevy pohybové energie vidíme všude kolem sebe. Proudící voda v řece nebo vítr v atmosféře nesou obrovské množství pohybové energie, kterou lze využít. Zvuk je vlnění, které se šíří prostředím právě přenosem pohybové energie mezi částicemi tohoto prostředí. [22]

💡 Přeměny a praktické využití

Podle zákona zachování energie nemůže energie vzniknout ani zaniknout, pouze se může přeměňovat z jedné formy na druhou. [23] Pohybová energie je ústředním bodem mnoha těchto přeměn.

Přeměna z polohové energie: Když těleso padá, jeho polohová energie klesá a přeměňuje se na energii pohybovou. Na tomto principu fungují vodní elektrárny, kde polohová energie vody v přehradní nádrži je přeměněna na pohybovou energii proudící vody, která roztáčí turbíny. [24]
Přeměna na jiné formy: Při brzdění se pohybová energie vozidla přeměňuje třením v brzdách na teplo. U elektromobilů a hybridních vozidel umožňuje systém rekuperačního brzdění přeměnit část pohybové energie zpět na elektrickou energii a uložit ji do baterie. [25]
Využití v energetice: Větrné elektrárny přeměňují pohybovou energii větru na rotační energii vrtule a následně na elektřinu. [26]
Ukládání energie: Setrvačníky jsou zařízení navržená k ukládání energie ve formě rotační pohybové energie. Roztočený masivní rotor si uchovává energii, kterou lze později opět odebrat. Využívají se například ve zdrojích nepřerušovaného napájení (UPS) nebo v systémech KERS ve Formuli 1. [27]

Zdroje